---

In order to push the envelope of science, robotics experimentalists must be fluent in a variety of topics — from materials properties, mechanics, and electronics, to a seemingly endless variety of computing methods. In each case, it’s short-sighted to focus on the technology de jour without developing an appreciation of the relevant underlying building blocks or first principles. There’s something to be said, for example, for building your first robotic crawler out of balsa wood instead of carbon fiber. You’ll have to pay attention to load bearing areas, torsion forces, and maximum payload, for example, instead of just designing for aesthetics.

You should consider computing in the manner. For example, it’s important to appreciate that models of computing have evolved as a function of the technology as well as the culture and maturity of users. Consider that the abacus, slide rule, and analog computer have come and (to a large degree) gone. From a STEM or robotics perspective, much can be gleaned by developing the mental models required to work with these “antiquated” technologies with those associated with contemporary microcomputer methods. This article (the first in a three-part series) considers the mental math skills that you can develop by learning and operating the Japanese abacus (Figure 1).

FIGURE 1. A modern Japanese abacus.

---

A Bit of History

The abacus was popular among the ancient Greeks, Romans, and Chinese, but the point of origin has been obscured by time. For example, while many in the west consider the abacus an eastern invention, the ancient Romans relied on a reckoning table called the abax — a term derived from Greek. Regardless of which culture invented the abacus, it’s remarkable that the technology has managed to survive in the era of the modern calculator, personal computer, and smartphone. Many students and teachers in the west are surprised to learn that in many parts of Asia — including China, South Korea, and Japan — the abacus is still used to introduce students to math and develop their mental math skills.

Until relatively recently, the abacus was used in the US. For example, in elementary school, I learned math with the aid of a colorful six column Chinese abacus. Although the Chinese abacus is more powerful and capable of more operations, I prefer the simpler Japanese version — especially for simple addition and, to a point, subtraction. At this point in my life, I’m not trying to develop new math skills as much as I am trying to slow the loss of math skills that I’ve developed over a lifetime teaching and working in science.

Figure 2 shows a few columns of a modern 27-column Japanese abacus. The Japanese abacus has changed little since the Chinese abacus was imported into Japan over 500 years ago. From right to left, columns or rods represent increasing values in powers of ten. In other words, the first four columns could represent (from right to left) ones, tens, hundreds, and thousands. Alternatively, they could read thousandths, hundredths, tenths, and ones. If you’re using an abacus for tabulating anything other than adding interplanetary distances, you can get by with a dozen or so columns. However, the extra columns come in handy when you’re faced with multiplication and division problems.

FIGURE 2. Close-up of a modern Japanese abacus, with one birch bead in the upper deck and four in the lower deck.

---

Within the upper deck, there is a single bead in each column with a value of five. There are four beads within each column on the lower deck with a value of one per bead. Together, top and lower deck beads in each row can represent 0 through 9. More on that later.

A good quality abacus costs about as much as a typical pocket calculator. For example, I paid about $30 for the abacus shown in Figure 2 (a Tomoe Standard) in a Tokyo office supply store. You may recognize the Tomoe brand as the maker of high quality paper. The same model abacus is available for $68 on Amazon.

No-name models with fewer columns and mechanical reset buttons are available on Amazon starting at about $20. The reset button which zeros the abacus between operations is nice but not necessary for the operation of the abacus.

As you can see from Figure 2, each column holds one bead on the upper deck and four beads on the lower deck. This contrasts with a Chinese abacus, which has two beads on the top deck and five plastic beads along the lower deck. In the US, the Japanese abacus seems to be the most popular, perhaps because there is a variety of books written in English on the Japanese abacus for young adults. The “Complete Abacus Mind Math” by the Abacus Training Foundation 2017 provides a gentle introduction to addition and subtraction on the Japanese abacus. If you’re not into books, then check out the Japanese abacus tutorial on WikiHow.com.

Faced with problems in addition and subtraction, in the right hands an abacus can hold its own in terms of speed and accuracy compared with someone equipped with an electronic calculator. In contrast, when faced with multiplication, division, and derivation of roots, just about anyone with an electronic calculator or smartphone with Siri or other voice assistant has the advantage. The point of learning an abacus is not to compete with the latest CPU in all levels of math, but to develop and sharpen your own mental math skills.

Think about it. Pressing abstract symbols on a numeric keypad and then reading the answer may develop some muscle memory, but it isn’t going to improve your math skills. Compare that exercise to directly manipulating columns of ones, tens, hundreds, thousands, and so on, and reading the intermediate as well as final answers on those same columns. Now that’s going to stick!

Hands On

Now that you’re familiar with the layout of the abacus, let’s practice reading the abacus and then work up to simple addition and subtraction.

Reading the Abacus

Study Figures 3-7 until you understand how to read the abacus. For example, Figure 3 shows the abacus at zero, ready for operation. The beads that have been moved from the start or zero position are shown in blue. Beads that remain in the original position are shown in yellow. Also, note that the abacus is normally read from left to right.

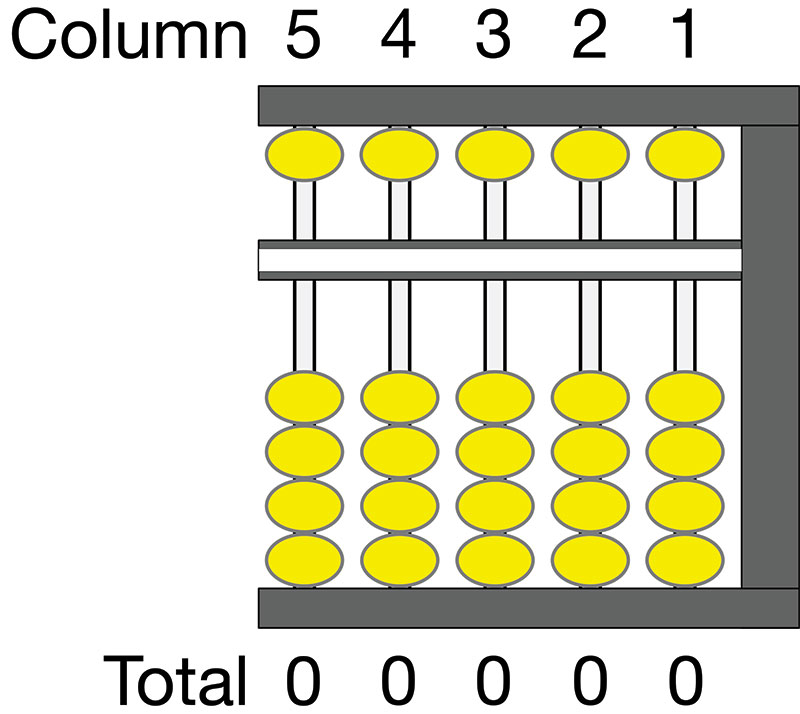
FIGURE 3. Abacus at start or zero position, value 0.

---

In Figure 4, the abacus reads 6,437. Column 5, the leftmost column, is the ten thousands column. It’s at the zero position. Moving to the right is column 4, the thousands column. There is one bead representing 1,000 moved up in the lower deck and one bead representing 5,000 moved down in the upper deck. Together, the upper and lower deck beads in column 4 total 6,000.

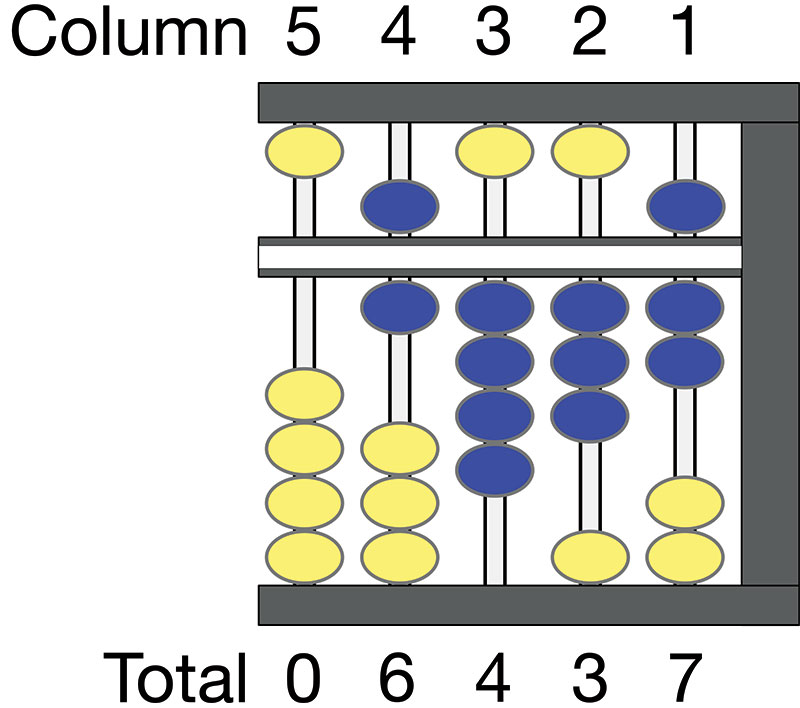
FIGURE 4. Abacus showing value 6,437. Original bead positions shown in yellow; beads that have been moved are shown in blue.

---

Next, moving one column to the right is column 3, the hundreds column. There are four beads in the lower deck pushed up, representing 400.

Again, moving to the right, column 2 is the tens column. There are three beads pushed up in the lower deck, representing 30.

To the far right, in the 1’s column, there are two beads in the lower deck pushed up, or two. Also, the bead in the top deck is moved down, adding five to the two from the lower deck, for a total of seven. So, putting the sequence together, we get 6,437.

Figure 5 shows the abacus set to 10,528. In the leftmost ten thousands column, a single bead from the lower deck is moved up, representing 10,000. Column 4 is unchanged, representing zero in the thousands column. Column 3 shows one bead moved downward in the upper deck, representing 500. Column 2 shows two beads moved upward in the tens column for 20. Finally, to column 1, which shows one bead from the upper deck moved down for five, and three beads from the lower deck representing three for a total of eight.

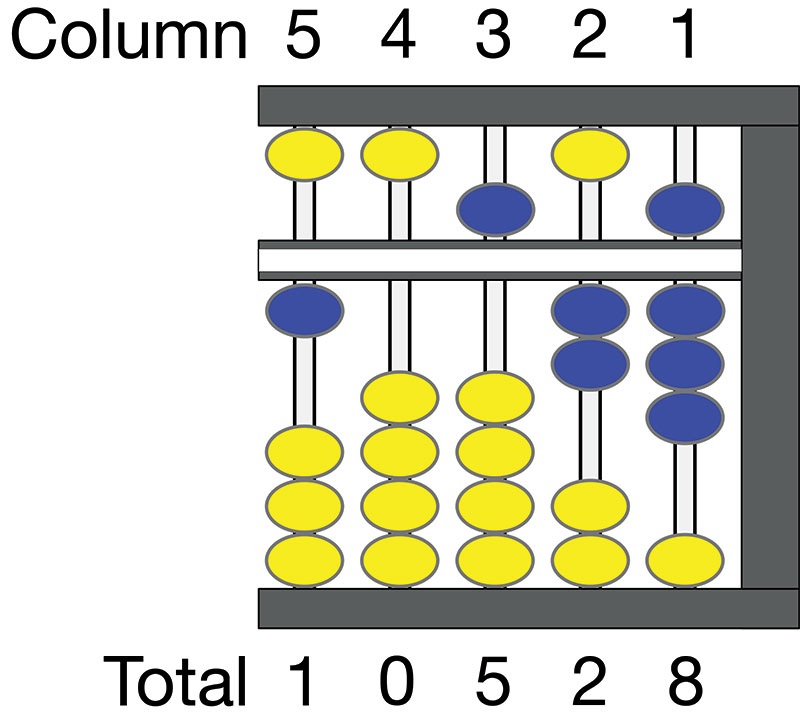
FIGURE 5. Abacus showing value 10,528.

---

In Figure 6, the abacus shows 9,792. Recall that the yellow beads haven’t been moved from the zero position. As such, the total for column 5 is zero. In column 4, the upper deck bead is pushed down, representing 5,000 and four from the lower deck are pushed up, representing 4,000, for a total of 9,000. In column 3, the bead in the upper deck is moved down for 500 and two from the bottom deck for 200 for a total of 700. In column 2, the tens column, the upper deck bead is pushed down for 50 and the four lower deck beads are pushed up for 40 and a total of 90. Column 1 (the single digits column) has two beads in the lower deck pushed up for a value of two.

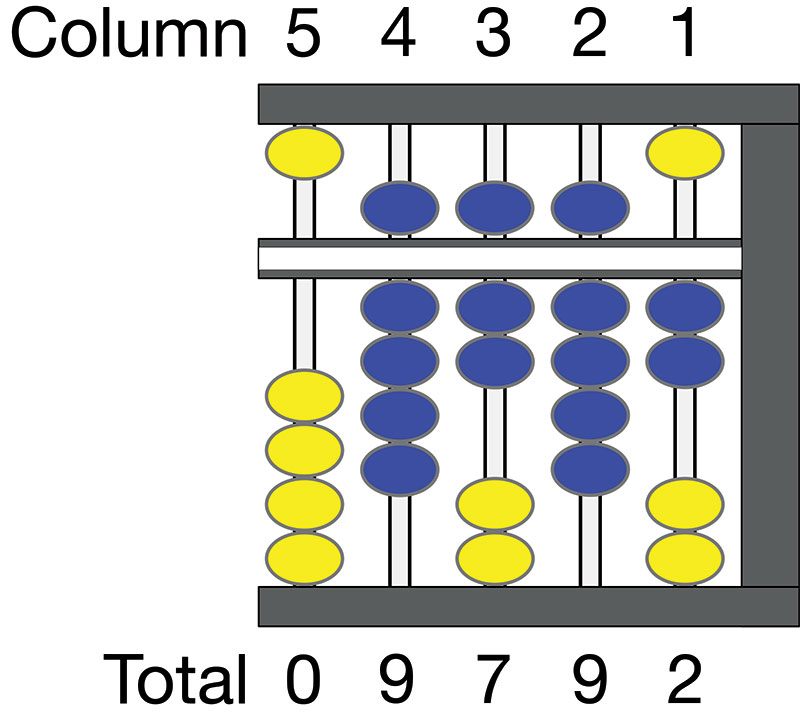
FIGURE 6. Abacus showing value 9,792.

---

By now, you should be able to read Figure 7 on your own. Starting with column 5, we have five (top) plus two (bottom) for 70,000. Next is three on the bottom for 3,000. Column 3 has one bead in the bottom deck for 100. Column 2 has four beads in the bottom deck for 40, and column 1 has two beads in the bottom deck for two. The total is 73,142.

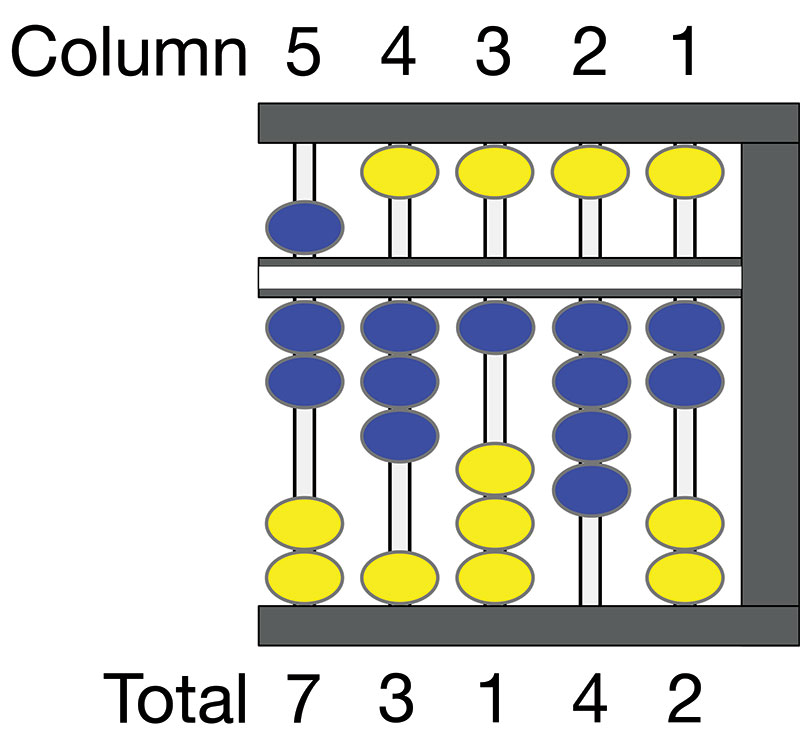
FIGURE 7. Abacus showing value 73,142.

---

Addition

Now, let’s do one addition problem. Building from the example above, let’s add 3,355 to 6,437, shown in Figure 8.

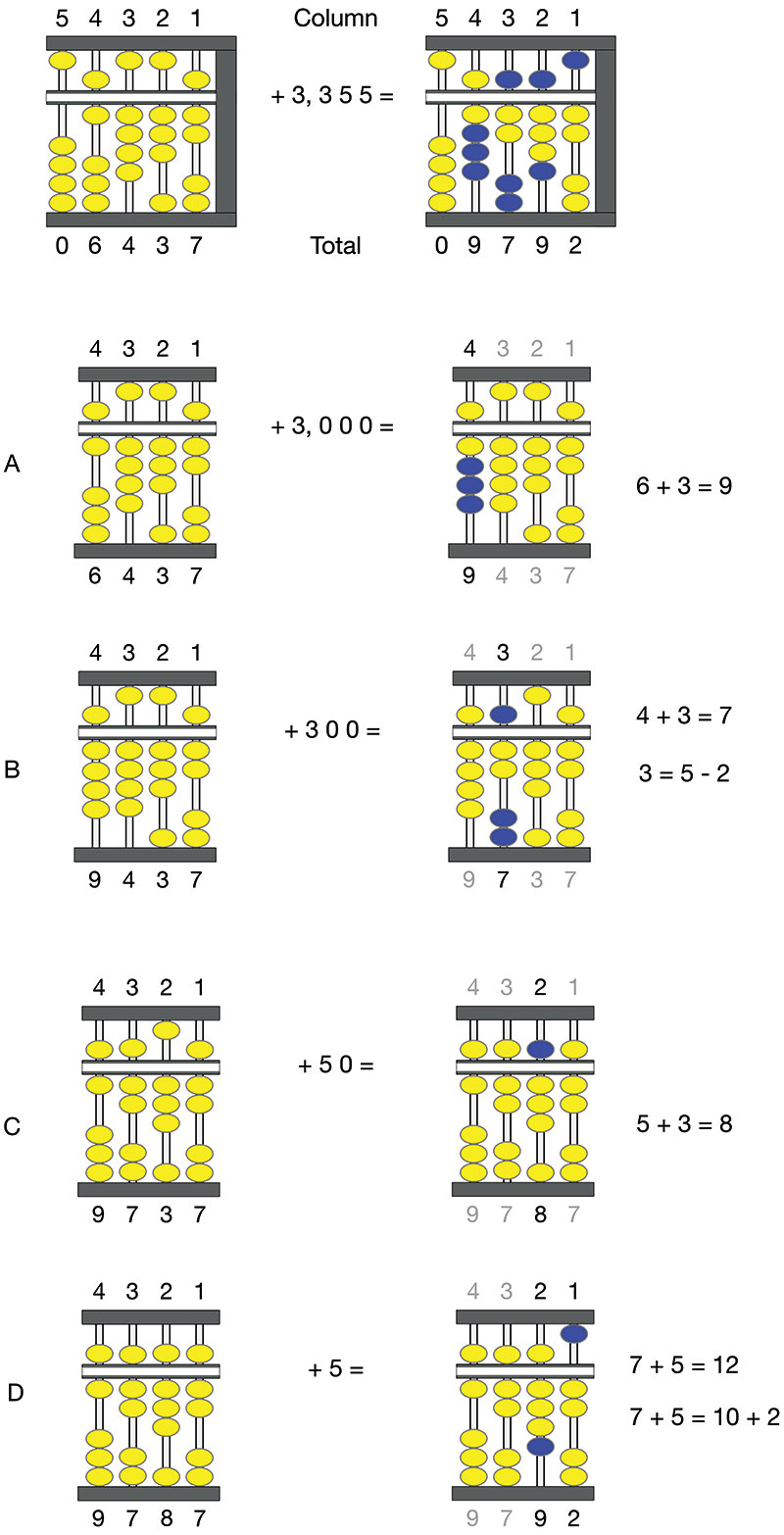
FIGURE 8. Adding 3,355 to 6,437 for a total of 9,792. Beads that move from one step to the next are shown in blue.

---

Moving from left to right, starting with column 5, there is nothing to add, and the column remains unchanged. For the next steps, refer to the image pairs labeled “A” though “D” in Figure 8. The moves — and the mental math — associated with each of these steps are as follows:

A. Add 3,000 to column 4. Push up the three beads in the lower deck, for a column total of nine. Not much in the way of mental math required here.
B. Add 300 to column 3. We need to add three beads to the lower deck, but there’s only one free bead. Let’s use the bead on the upper deck to get the equivalent of five free beads in the lower deck and then remove two beads. As a result, we add three to column 4, for a column total of seven. This operation may seem complex at first, but with a few minutes of mental math practice, it should become second nature. This mental math is a feature and benefit of the abacus. You can’t simply push or pull a bead here and there to come up with a solution.
C. Add 50 to column 2. This is a simple add, by pushing down the bead in the upper deck.
D. Add five to column 1. As with column 3, this addition requires some mental math. It involves a carryover that will alter the beads in adjacent column 2. Specifically, column 1 starts with a value of seven: five from the bead in the upper deck and two from two beads in the lower deck. Seven plus the additional five is 12, or 10 plus two. So, let’s give column 1 a value of two by moving the bead in the upper level up to the reset point and increment the tens column by one by moving one bead up in the lower level of column 2. That’s about as complex as addition gets on the abacus.

Subtraction

Because subtraction can be more complex than addition, let’s use a problem with fewer digits. As shown in Figure 9, our subtraction problem involves subtracting 386 from 463. This example shows how to handle the situation when we have to borrow from a column to the left to have enough beads to work with in the current column.

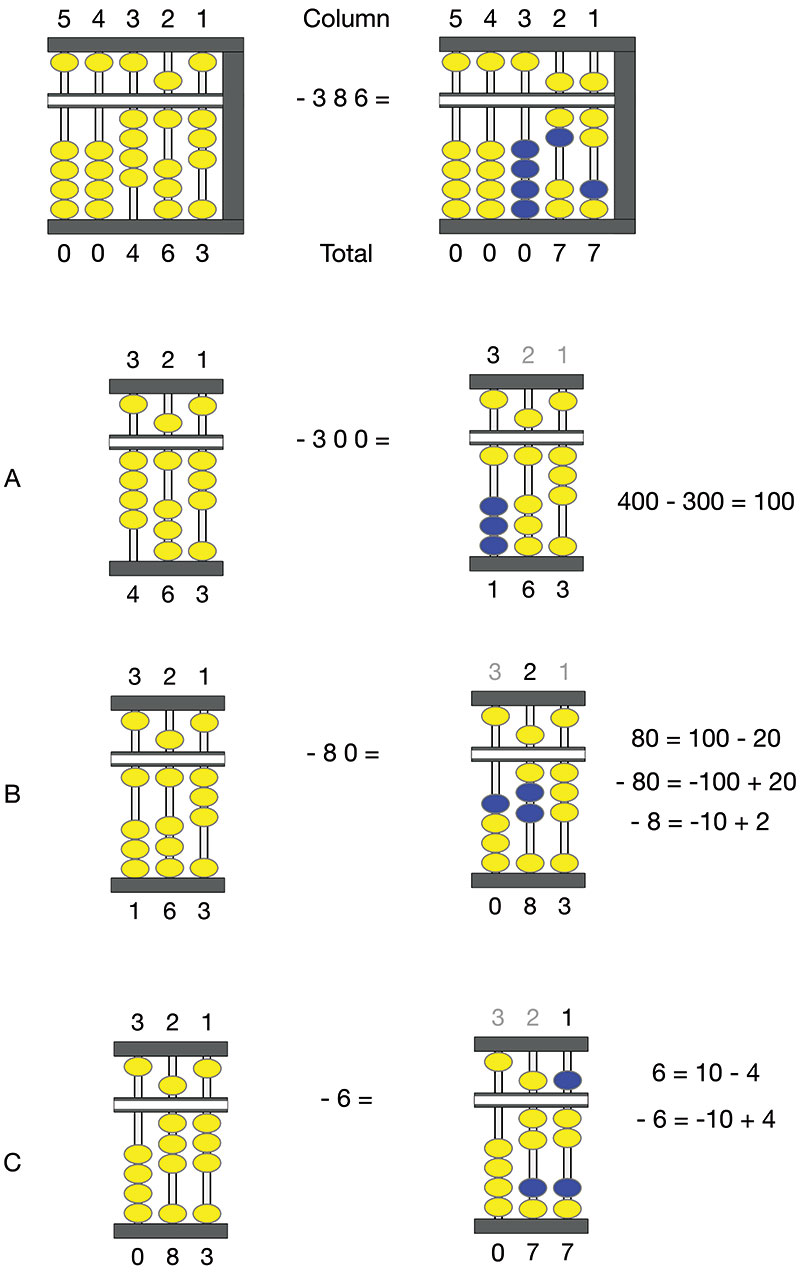
FIGURE 9. Subtracting 386 from 463 yields 77. Yellow beads are in their original position. Blue beads have been moved from their original position.

---

Again, working from left to right, we can ignore columns 4 and 5. Follow along with steps A, B, and C in Figure 9.

A. Subtract 300 from column 3. Slide three beads in the lower deck down to the starting position.
B. Subtract 80 from column 2. Since we don’t have enough beads, we have to borrow from column 3. Because 80 = 100 – 20, we move one bead up in column 3, subtracting 100, and adding 20 (i.e., two beads) to column 2.
C. Subtract six from column 1. Again, faced with a lack of beads, we have to borrow from the left adjacent column. Because 6 = 10 – 4, we get four beads in the one’s column for a bead in the ten’s column. Column 1 gains a top deck bead (i.e., the bead is moved down) and loses a lower deck bead (i.e., the bead is moved down) to become seven. Column 2 loses a bead to become seven.

Where to Go From Here

As you can see from the addition and subtraction examples above, working the abacus requires your full mental engagement in the mathematical process. Regular use should hone your single- and double-digit addition math skills as well as your appreciation for the power of ten.

You won’t get that level of engagement from mindlessly pressing the keys of a calculator. I’m not suggesting you toss your pocket calculator, but that you incorporate the abacus — at least for a while — into your mathematical life. Keep a magnetic version on your refrigerator door to track daily caloric intake, for example.

If the abacus tickles your interest in math and alternative computing models, you owe it to yourself to purchase an inexpensive Japanese or Chinese abacus and go through the basics covered above. The abacus also makes a great gift for the budding robotics experimentalist in your family.

In Part 2, we’ll look at another important mathematical computing model that’s largely — but not completely — come and gone: the slide rule. In Part 3 of the series, we’ll build and learn to use an electronic analog computer. As in Part 1, in each case, you’ll see that there’s something to be learned by thinking outside of the digital computer box.  SV

---